题目分析

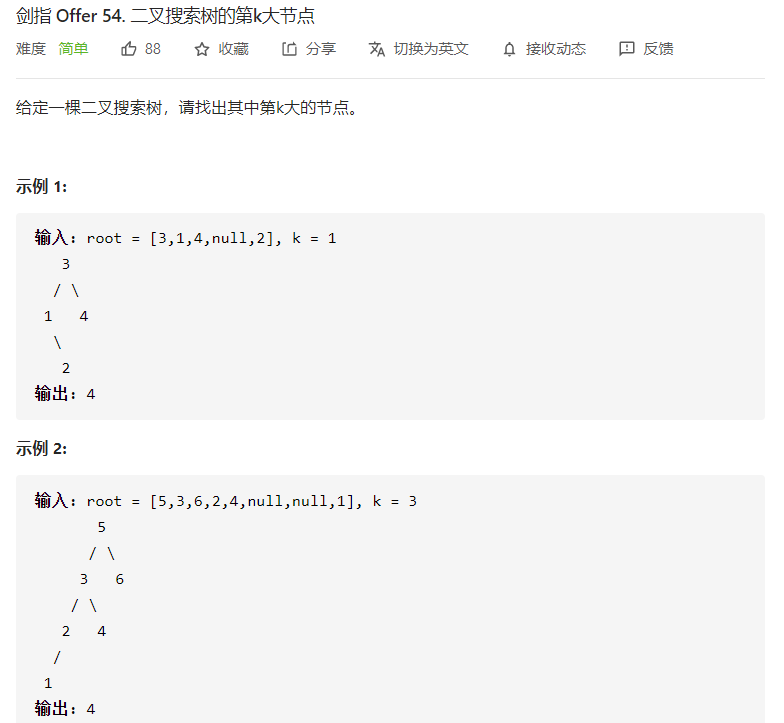
二叉搜索树第k大的节点，这个题目还是非常简单的，除了常规解法还给小伙伴们推荐一个奇妙的方法，小伙伴先尝试如何求解。

递归

根据二叉搜索树的规律，使用中序遍历访问所有节点，将节点存放在容器中，然后取出容器倒数第k个值即可。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

#include<iostream>
#include<vector>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        vector<int> res;
        inorder(root, res);
        return res[res.size() - k];
    }

    void inorder(TreeNode* node, vector<int>& v) {
        if (!node) {
            return;
        }
        inorder(node->left, v);
        v.push_back(node->val);
        inorder(node->right, v);
    }
};

优化递归

本题还有一个更加巧妙的方法，我们要求第k大的元素，如果按照中序遍历的方法，需要遍历所有节点，如果k=1，我们也需要访问所有的节点，这样是不划算的。虽然最坏情况的时间复杂度都是$O(n)$，但是我们不希望这么做。

我们可以逆中序遍历进行访问，使用一个计数器cnt，访问一个节点cnt++，当cnt=k的时候停止递归。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

#include<iostream>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        int res = 0, cnt = 0;
        inorder(root, res, cnt, k);
        return res;
    }

    void inorder(TreeNode* node, int& res, int &cnt, int k) {
        if (!node) {
            return;
        }
        inorder(node->right, res, cnt, k);
        if (++cnt == k) res = node->val;
        if (cnt >= k) return;
        inorder(node->left, res, cnt, k);
    }
};

迭代

中序遍历是可以通过迭代进行的，先访问左子树，在访问左子树之前将根节点加入容器，然后容器的尾部就是最左端的节点，取出该节点，访问其右子树，在访问右子树的过程中也是先访问其左子树。

在这里也是按照一个逆中序遍历的顺序进行的，代码也比较简单，小伙伴直接看代码即可。

算法的**时间复杂度为$O(n)$，空间复杂度为$O(n)$**。

#include<iostream>
#include<vector>

using namespace std;

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    int kthLargest(TreeNode* root, int k) {
        vector<TreeNode*> v;
        TreeNode* cur = root;
        while (cur || v.size()) {
            while (cur) {
                v.push_back(cur);
                cur = cur->right;
            }
            cur = v.back();
            v.pop_back();
            if (--k == 0) return cur->val;
            cur = cur->left;
        }
        return root->val;
    }
};

刷题总结

中序遍历的递归求解是大家都比较清楚的，但是如何迭代求解是大多数人都没有了解过的，迭代求解思路奇妙，代码量相对递归求解较长，作为拓展知识。